Scalable and Efficient Speech Enhancement Using Modified Cold Diffusion

As we’ve proposed in the BLOOM-Net project, scalability matters. Just to reiterate the argument here once again, the main issue with the current deep learning-based models for speech enhancement is that they tend to be trained for just one particular goal: best-effort enhancement. The model architecture is fixed from the get-go and is trained to estimate the clean speech target no matter what. With BLOOM-Net, we showed that it’s possible to come up with a flexible model architecture that scales up and down freely, depending on the system’s resource budget. For example, if the system lacks computational power (e.g., a phone running out of battery), the model can shrink to its minimal version, i.e., battery saving mode, which is still trained to produce an acceptable enhancement result. We actually see many such scalable systems in other applications, e.g., the video codec that lowers its bitrate when the network bandwidth is not good enough, a cordless vacuum that lowers its RPM when the floor is already clean enough, etc.

In this scalable and efficient speech enhancement (SESE) project, I delved into the concept of scalability from the perspective of the recently proposed concept of cold diffusion1. Cold diffusion was originally proposed as a generative model that works with deterministic noise input, and it was later applied to speech enhancement, showing promising results2 due to its convenient flexibility that it accepts any type of noise as input, i.e., the noisy speech. Although we relate the proposed method to cold diffusion’s sampling process, we would like to note that the proposed method presents a totally different sampling process, which we argue is more efficient and convenient to interpret than cold diffusion.

One-shot speech enhancement (SE)

Let’s begin with the traditional SE system. In the simplest denoising case, suppose that the clean speech signal \bm{s} is contaminated by a noise source \bm{n}, which forms the noisy speech utterance \bm{x} (see the figure above where these variables are represented in a vector space). Given the noisy utterance, which is the only information available during the test time, the SE model’s job is to recover the clean speech \bm{s}, i.e., the estimate \hat{\bm{s}} is trained to be as similar as possible to \bm{s}. Of course, a very capable model can be defined with a large architecture that performs this nonlinear mapping pretty successfully. At the same time, for a resource-constrained environment, a small model is tasked to do its best. We denote these SE models by R(\bm{x}). In the figure above, for example, two R(\bm x) cases are shown to represent the typical relationship between the model complexity and its performance.

We call this traditional SE method “one-shot” SE, because it does not involve any iterative process for its inference. Just a one-time inference routine of the neural network will produce an enhanced result. From the scalability perspective, the system has to maintain two different versions of the models that are selectively used depending on the resource constraint. In addition, there is a chance that the estimate \hat{\bm s} can be farther away from the original speech \bm s, if the small model is not capable of learning the complex mapping between \bm{x} and \bm{s}.

Cold Diffusion for SE

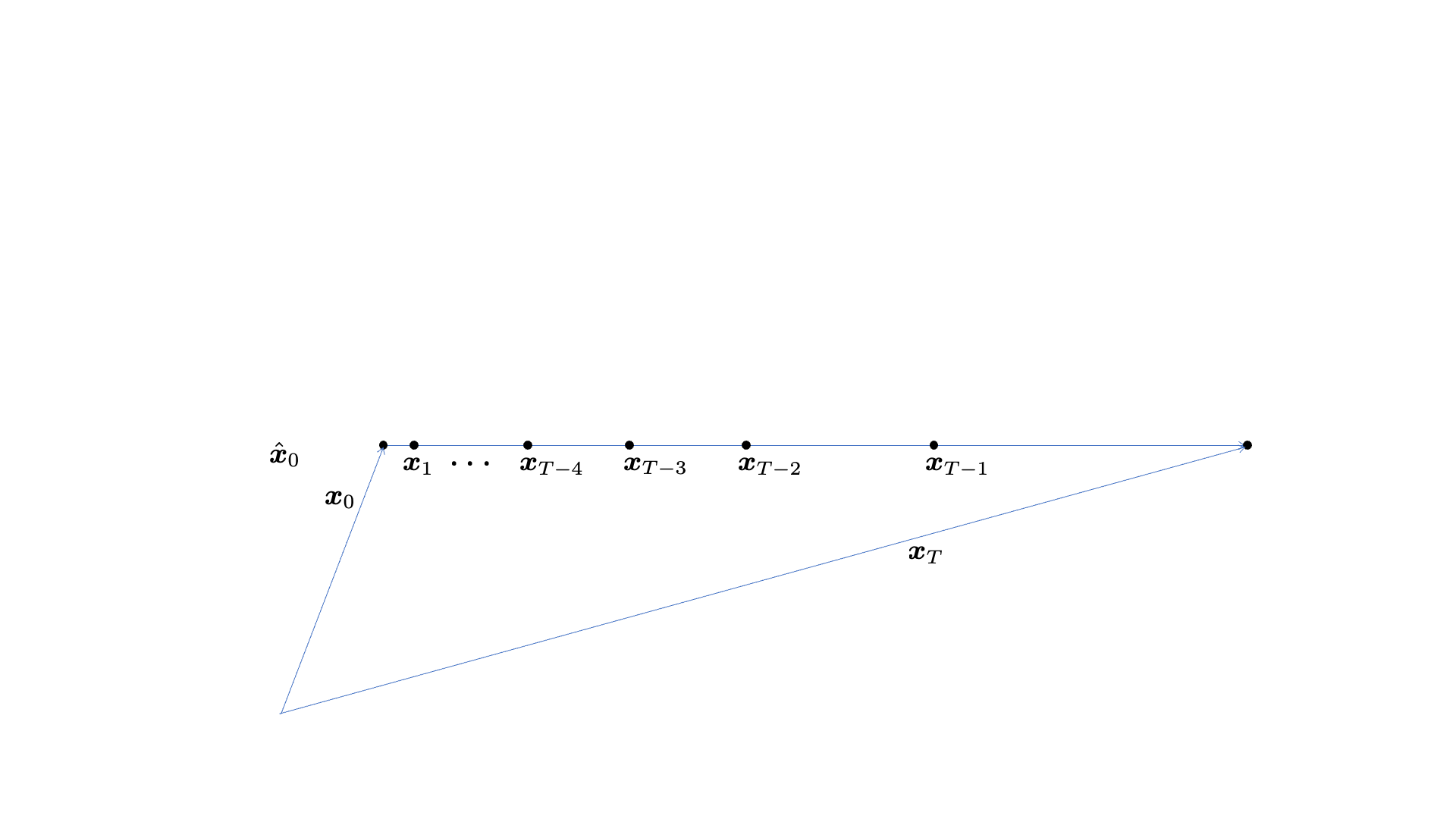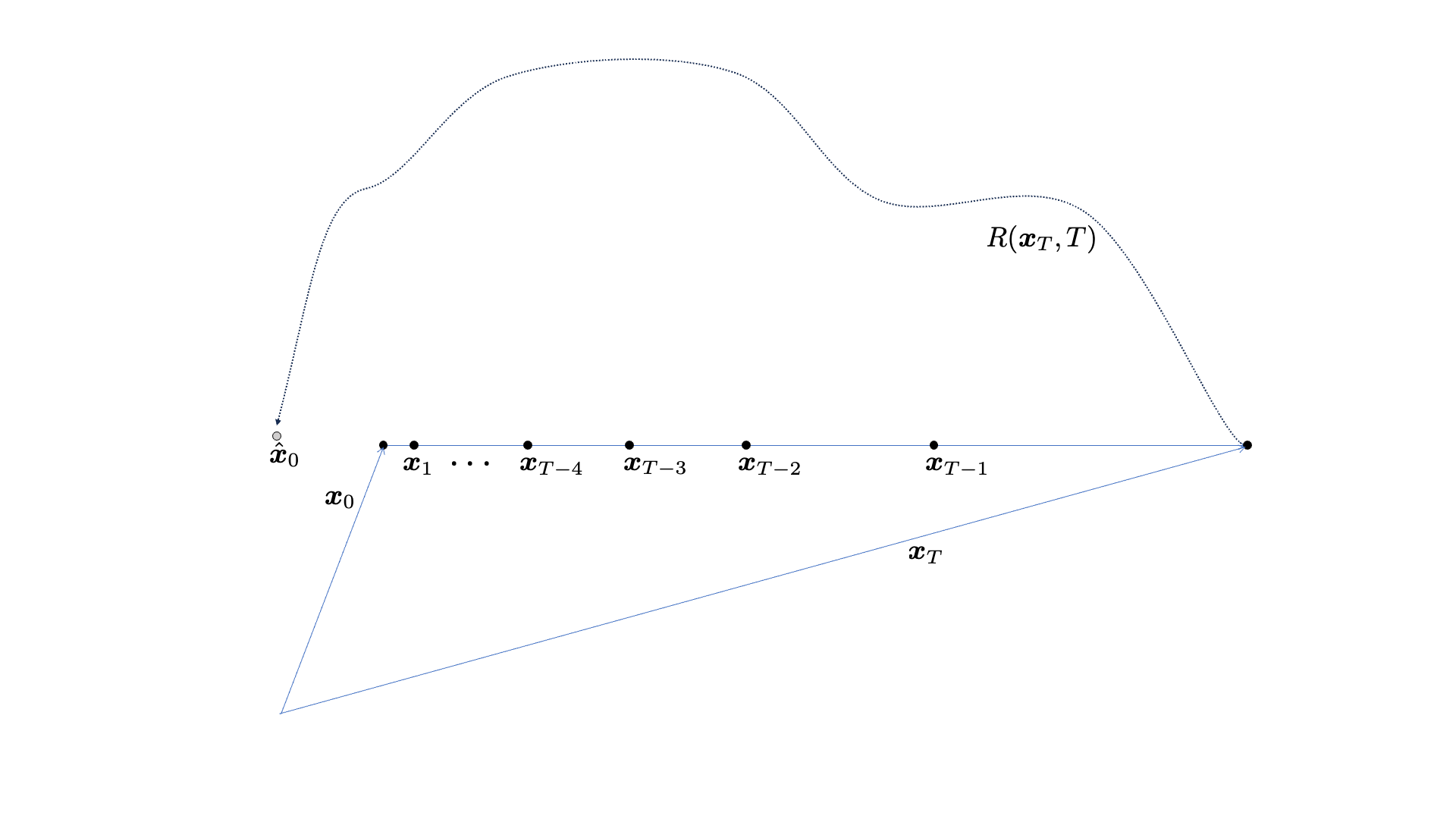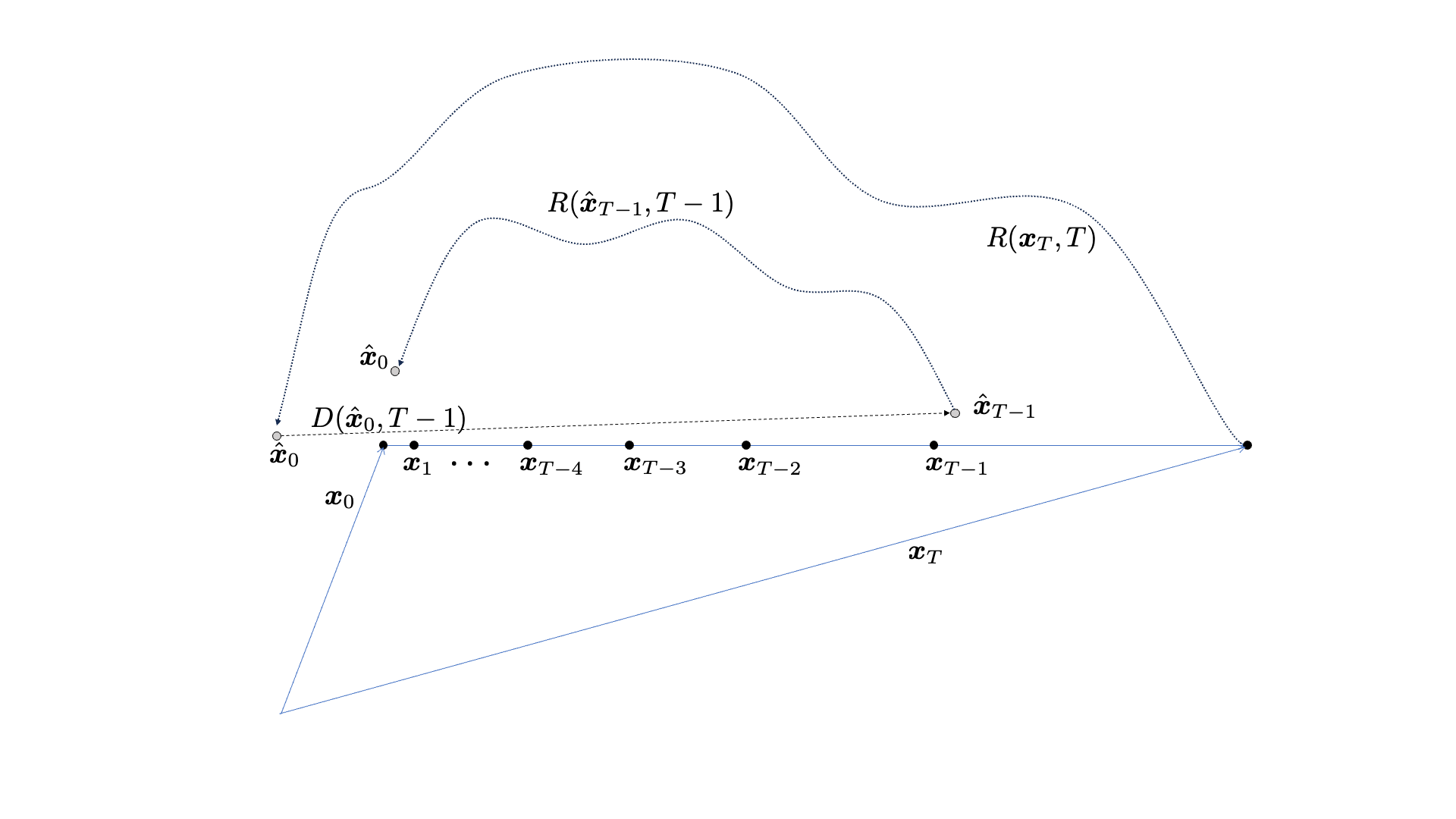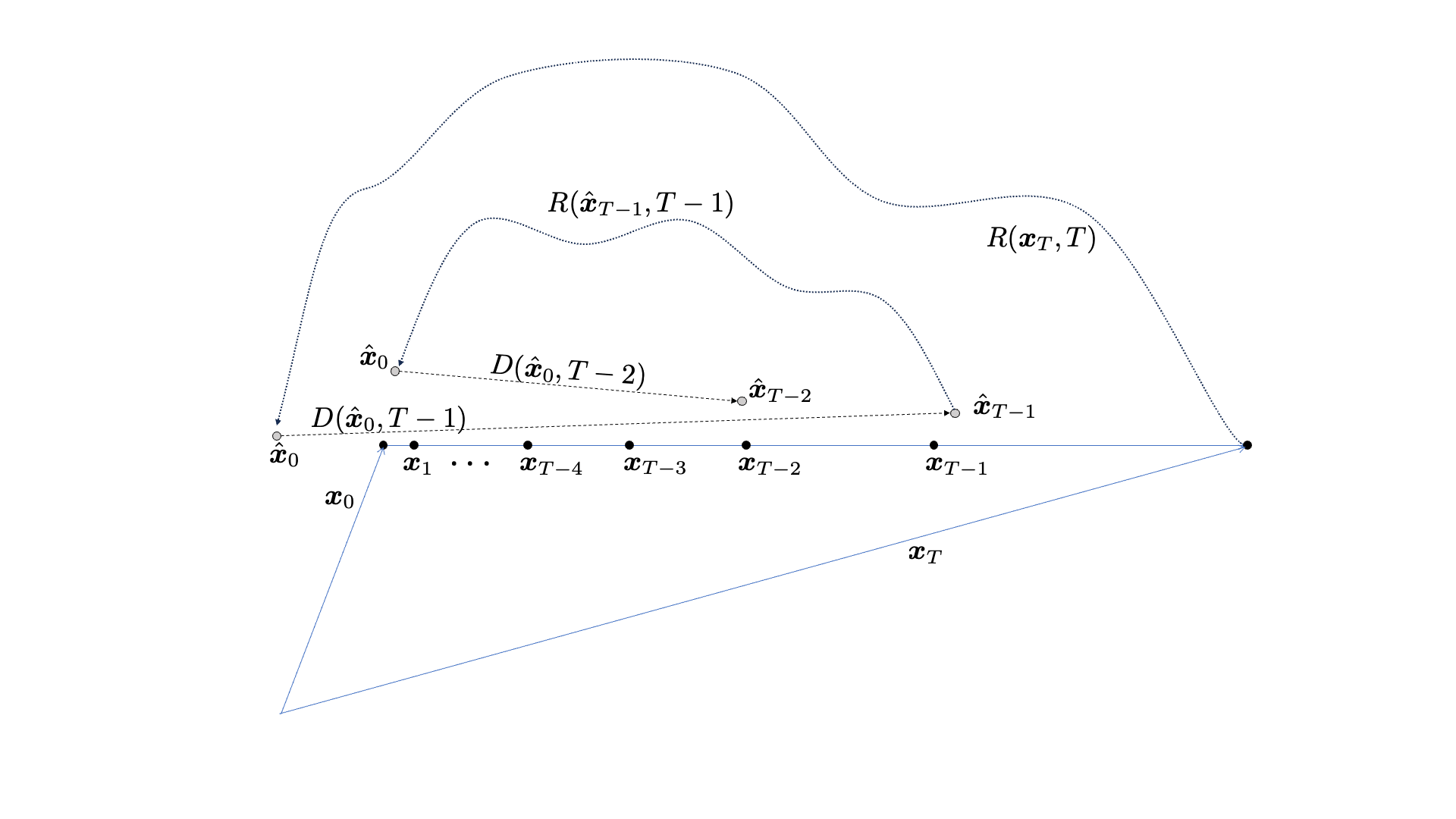
The cold diffusion method for SE does this job in an iterative fashion. It starts from the noisy utterance as the “noise” input to the reverse diffusion process. Since the reverse diffusion process consists of multiple sampling steps, we introduce the step-index t with \bm x_0 and \bm x_T being the target clean speech (i.e., \bm s) and input noisy speech (i.e., \bm x), respectively. It assumes that the intermediate sample \bm x_t is a linear combination of \bm x_0 and \bm x_T. For example, there is a degradation process that contaminates the clean speech \bm x_0 into any intermediate version \bm x_t, i.e., D(\bm x_0, t). The degradation function is controlled by the sampling step index t, which also defines the amount of degradation for the linear combination.

Then, the SE model performs the best-effort SE given any intermediate input \bm x_t. In the cold diffusion context, we call this the restoration function. The process begins with the initial input \bm x_T, whose enhancement result \hat{\bm x}_0 is fed back to the degradation function to estimate the next intermediate sample \hat{\bm x}_{T-1}—it’s only an estimate as the system doesn’t have access to clean speech \bm x_0, so instead, the degradation function has to use the estimated one, \hat{\bm x}_0. The sampling process repeats this cycle until it reaches \hat{\bm x}_1, which will be used as the final input to the restoration function R(\hat{\bm x}_1, 1).

The cold diffusion for SE paper2 has it’s own unfolding mechanism that prevents the propagation of reconstruction error, so it’s a little more complicated than the figure.

The main issues with this cold diffusion process are

  • The restoration function 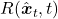R(\hat{\bm x}_t, t) is a generic one that needs to handle any intermediate input signals for all t. To this end, the model takes t as a conditioning input. While it’s a valid way to inform the model of the amount of denoising to be done, the model becomes larger to generalize well to all those use cases.
  • The restoration function always conducts the best-effort enhancement. In some applications, though, it might be too challenging of a target to achieve.

In other words, in cold diffusion, the sampling process always goes back to the clean target no matter where degradation step the sampling process is positioned. Given that it has to come back to the intermediate mixtures anyway via the degradation process, is there any better way to do this iterative restoration? What if the intermediate restoration step conducts a compromised, thus easier target?

The proposed SESE method

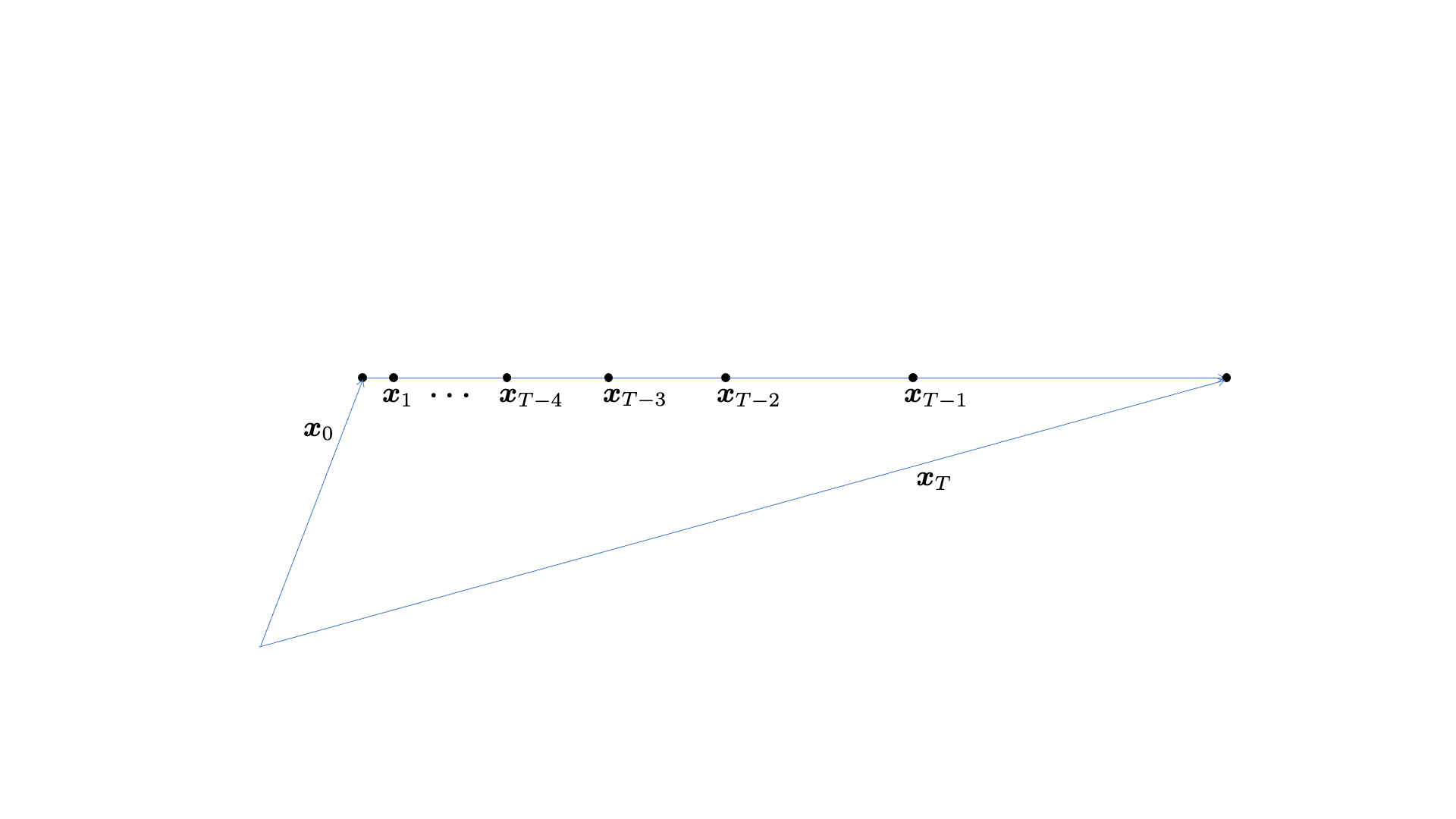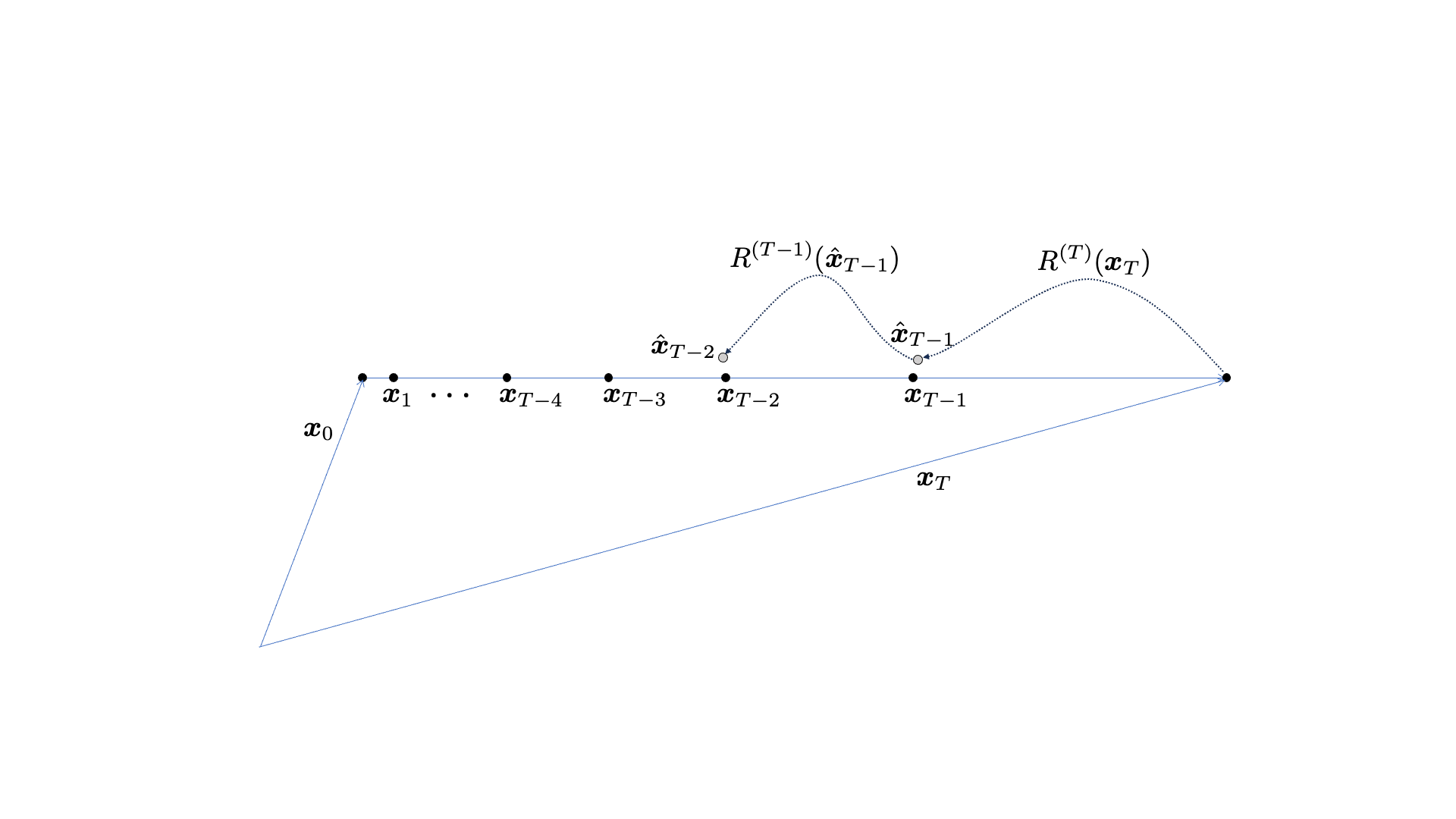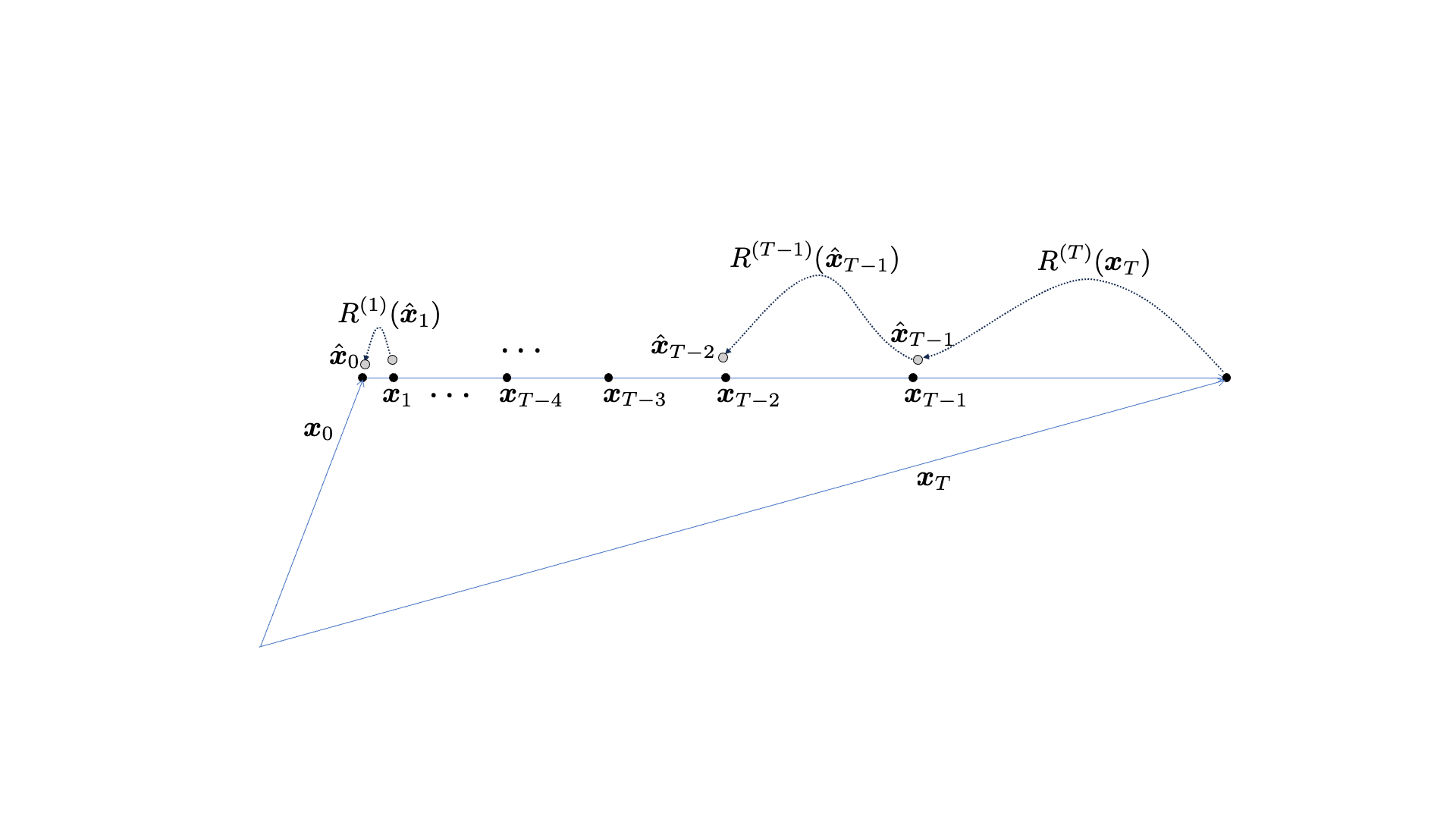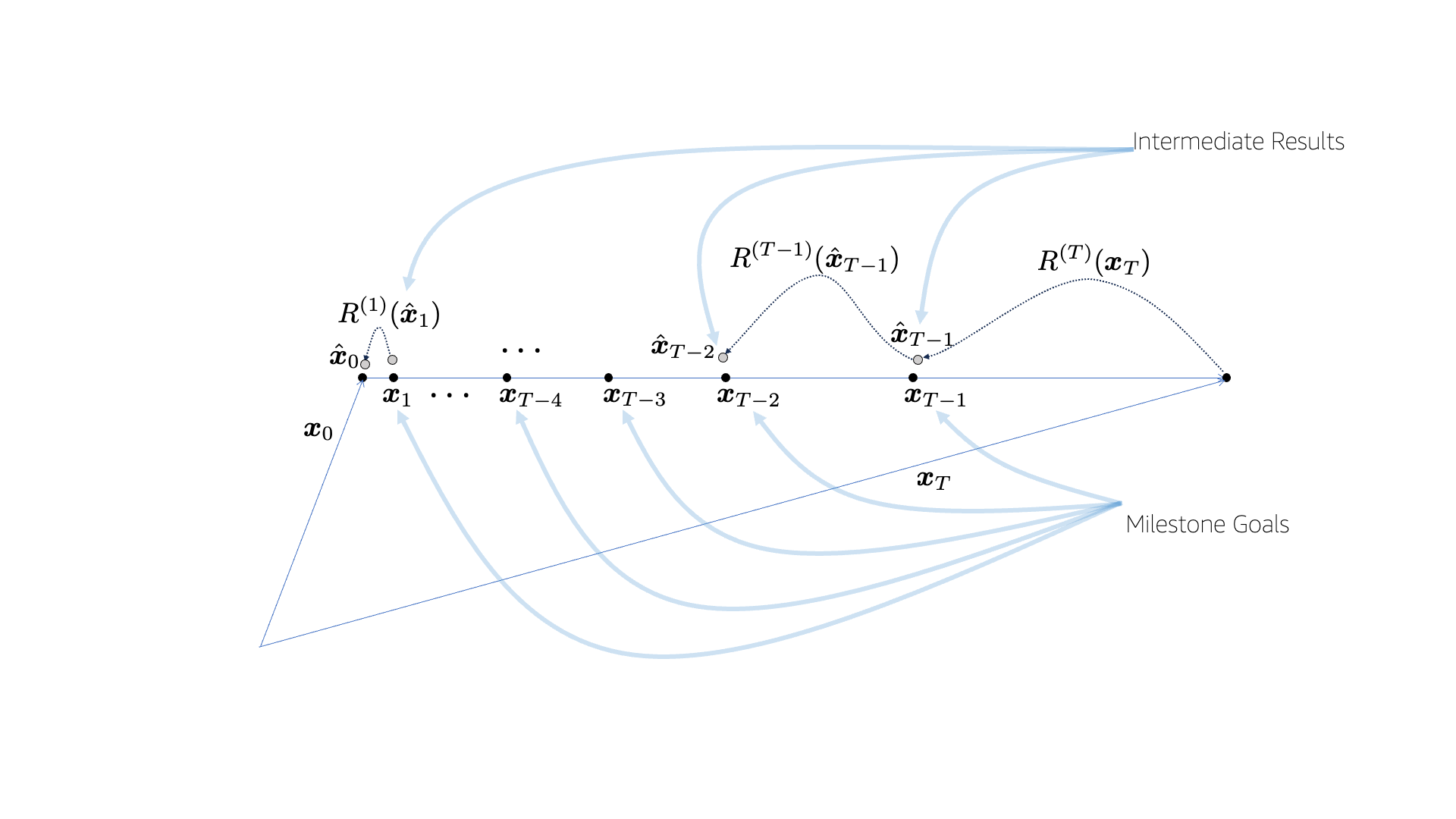
The proposed SESE method employs multiple restoration functions R^{(T)}(\bm x_T), \ldots, R^{(1)}(\bm x_1) each of which is responsible for the particular step’s denoising. So, eventually, the proposed SESE method drifted away from the original cold diffusion algorithm. These step-by-step restoration functions have some advantages.

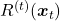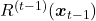  • Each restoration task learns a subtle change between R^{(t)}(\bm x_t) and R^{(t-1)}(\bm x_{t-1}). Since the input and target of mapping are on the smooth interpolation line, their difference is easier for the model to learn, leading to better approximation. We call these intermediate mixtures milestone goals.
  • The process can be redefined to learn the residual between the target and the input, i.e., 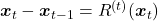\bm x_t-\bm x_{t-1}=R^{(t)}(\bm x_t), rather than the output directly. A well-known benefit introduced in the ResNet architecture. We cold this variation ResSESE.
  • Small neural network architectures are good enough to learn these mapping functions (0.58% of the cold diffusion model used for SE!).
  • The intermediate results are useful. These intermediate results are with less artifact, although they still contain the original noise source, which is louder when 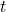t is large, while it can be suppressed further as 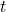t nears 0.
  • The model is scalable as the intermediate solutions are cheaper to produce.
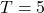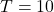  • We found that SESE requires fewer sampling steps. T=5 or T=10 gave good results.
  • From the learning perspective, this process can be seen as guided learning as the intermediate solutions are compared with the milestone goals multiple times, eventually leading to better performance.

For more information, please take a look at the paper.

Paper

Minje Kim and Trausti Kristjansson, “Scalable and Efficient Speech Enhancement Using Modified Cold Diffusion: a Residual Learning Approach,” in Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Seoul, Korea, Apr. 14-19, 2024 [pdf]

Sound Examples

In the following examples, you will see three ResSESE results near the end of the process, e.g., \hat{\bm x}_2, \hat{\bm x}_1, \hat{\bm x}_0, when the total number of sampling steps is T=5. Here, to help you understand the intermediate nature of the input, I made up a concept called signal-to-mixture (SMR) ratio, which is -INF if the input is the pure mixture \bm{x}_T and goes up as the clean speech is mixed up more as t reaches 0. These SMR values are the input’s noisiness at the given step t and the sound example is shown as a result of that step’s processing by R^{(t)}(\hat{\bm{x}}_t). For example, one of the presented examples \hat{\bm x}_2 is step t=3‘s result via R^{(3)}(\hat{\bm{x}}_3), where \hat{\bm{x}}_3‘s SMR is -6.1 dB, meaning that \bm{x}_T was mixed in a lot more than \bm{x}_0 in \bm{x}_3.

Sound Examples #1

Sound Examples #2

More “final” examples can be found below. Here, T stands for the total number of steps during the diffusion process, while \tau is the index within the process, i.e., when \tau=T, the inverse diffusion process is finished.

Sound Examples #3

Ground Truth
Noisy Speech
ResSESE Final Result (\tau=10, T=10)
ResSESE Final Result (\tau=5, T=5)
SESE Final Result (\tau=10, T=10)

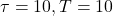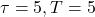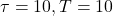Sound Examples #4

Ground Truth
Noisy Speech
ResSESE Final Result (\tau=10, T=10)
ResSESE Final Result (\tau=5, T=5)
SESE Final Result (\tau=10, T=10)

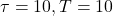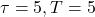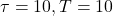Sound Examples #5

Ground Truth
Noisy Speech
ResSESE Final Result (\tau=10, T=10)
ResSESE Final Result (\tau=5, T=5)
SESE Final Result (\tau=10, T=10)

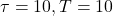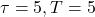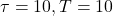Sound Examples #6

Ground Truth
Noisy Speech
ResSESE Final Result (\tau=10, T=10)
ResSESE Final Result (\tau=5, T=5)
SESE Final Result (\tau=10, T=10)

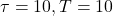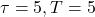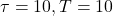Acknolwedgement

This work was done during my time at Amazon Lab126.

  1. Arpit Bansal, Eitan Borgnia, Hong-Min Chu, Jie S. Li, Hamid Kazemi, Furong Huang, Micah Goldblum, Jonas Geiping, Tom Goldstein, “Cold Diffusion: Inverting Arbitrary Image Transforms Without Noise,” arXiv:2208.09392, 2022.[↩]
  2. Hao Yen, François G. Germain, Gordon Wichern, Jonathan Le Roux, “Cold Diffusion for Speech Enhancement,” IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), 2023.[↩][↩]